Масса обручального кольца
Обручальное кольцо — не простое украшенье…
(песня)
Обручальные кольца — пожалуй, самые распространенные ювелирные изделия. Изготавливаются они просто, даже и вручную, и, казалось бы, зачем огород городить? Но дело осложняется одной весьма распространенной просьбой заказчиков: точно уложиться в вес того металла, который они принесли. (Если к вам пришли такие заказчики, дайте им прочитать эту статью, и возможно тогда они не будут столь категоричны.)
Под обручальным кольцом мы будем здесь подразумеваеть классический его вид: гладкое кольцо из полукруглого проката. И хоть масса кольца полукруглого сечения уже была нами вычислена в предыдущей статье, однако, там не были учтены некоторые нюансы.
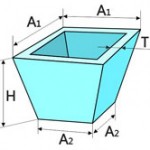
Во-первых, профиль ручья вальцов совсем не обязан быть именно половиной круга, чаще всего это только сегмент. Во-вторых, не обязательно прокатывать заготовку до конца, то есть, до смыкания валов, поэтому сечение проката в общем случае может выглядеть так, как показано на первой картинке.
Сначала договоримся называть сечение ручья вальцов (просвет между сомкнутыми валами) — «профилем», а заготовку, пропущенную через этот ручей, — «прокатом». Теперь обозначим интересующие нас величины:
— ширина проката;
— толщина проката .
— ширина профиля, она же длина хорды, она же максимальная ширина проката;
— глубина профиля, она же высота сегмента, она же минимальная толщина проката;
— размер кольца, то есть, его внутренний диаметр;
— плотность материала.
И, как повелось, все размеры будем измерять в миллиметрах, а плотность — в граммах на кубический сантиметр.
1. Основная задача
Основная задача — имея все эти параметры, найти массу кольца. Масса, как это ни удивительно, есть произведение плотности и объёма: 
Объем кольца — произведение площади его сечения и длины заготовки: 
Длина заготовки для любого кольца вычисляется по формуле 
Площадь сечения в общем случае, как видно на первой картинке, состоит из площади сегмента и площади прямоугольника.
Для определения площади сегмента нам никак не обойтись без радиуса круга, частью которого этот сегмент является. Для этого нам послужат параметры профиля, вторая картинка и статья Геометрия круга, а точнее — ее пункт 9, где даны длина хорды и высота сегмента. В применении к нашему профилю получаем 
и радиус кривизны 
.
Теперь мы можем вычислить площадь сегмента по третьей картинке. Возьмем площадь сектора и вычтем из нее площадь треугольника: 
. Заметим, что 
здесь имеет уже другое значение, чем на предыдущей картинке, а именно 
. Площадь прямоугольника составит 
. Прибавим к ней площадь сегмента и после небольших преобразований получим формулу для площади сечения нашего кольца:
Теперь остается перемножить 
, 
и 
, и мы получим массу кольца.
2. Незадача
Всё бы хорошо, да нет в природе ничего идеального! Есть две причины, по которым реальная масса кольца практически всегда отличается от расчетной.
- Форма поперечного сечения проката не совпадает с той геометрически точной формой, которая изображена на первом рисунке и по которой мы производили расчет. Эта форма зависит от начального профиля заготовки (квадрат, прямоугольник, круг и пр.), начальных размеров заготовки и даже от того, как часто вы ее отжигаете в процессе вальцовки.
- Неизбежные потери массы при обработке поверхности — шлифовке и полировке.
На четвертом рисунке приблизительно изображена реальная форма сечения проката. Интуитивно понятно, что отклонение реальной площади сечения от идеальной (которая обозначена пунктиром) — тем больше, чем больше разница между 
и 
, а также между 
и 
. Обозначим эту разницу 
и 
. Учитывая, что здесь мы имеем дело с малыми величинами относительно всей площади сечения, предположим самый простой вариант: линейную зависимость коэффициента поправки 
от этих двух величин: 
,
где 
, 
и 
— коэффициенты, которые нужно определить экспериментально. Будучи человеком упертым, я это сделал и получил следующие результаты: 
, 
, 
.
Но, к сожалению, эти значения не универсальны. Они соответствуют конкретно моим приемам работы и оборудованию, а для другого мастера наверняка будут другими.
Вторая напасть — потери при полировке — вещь тоже индивидуальная и тоже может быть определена только опытным путем.
Вывод: относитесь к значениям массы, вычисленным по вышеприведенным формулам, как к приблизительным, а коэффициент поправки определяйте для себя, набирая собственную статистику.
(Забегая вперед, и пророчески предвидя, что никто по этим формулам вручную ничего считать не станет, советую для вычисления массы обручальных колец обратиться к моей программе RingMass.)
3. Дополнительная задача
И ведь это еще не всё! Задача «вписаться» в нужную массу кольца при заданных размере и ширине выливается в задачу определения толщины проката. То есть, требуется определить, до какой толщины нужно катать заготовку, чтобы масса кольца получилась какая надо.
Напрашивается простой способ решения: из формулы для массы кольца нужно найти толщину проката, которая будет выражена через все остальные параметры. Но тут вмешивается та самая «незадача» с поправкой. Дело в том, что величина поправки зависит в том числе и от искомой нами толщины проката, что сильно усложняет решение.
Поэтому я даже не буду приводить тут эти немыслимые выражения, а сразу отошлю вас к программе RingMass, которая решает эту задачу не через формулы, а «по-программному», методом последовательных приближений.
